معاملات لحظه ای در ارزهای دیجیتال + بازده کوتاه مدت

معاملات لحظه ای در بازار ارز های رمز نگاری شده: بازده کوتاه مدت و مزایای ایجاد تنوع

چکیده

ما برای حضور اثرات تحرک آنی در بازار ارز های رمزنگاری شده آزمایش می کنیم و همبستگی شرطی پویای (DCC) بازده بین نمونه های تغییر ارزهای رمزنگاری شده و دارایی های سنتی را تخمین می زنیم. ابتدا، نمونه های سرمایه گذاری مطابق استراتژی تغییر کلاسیک J / K ساخته می شود و از داده های روزانه دوازده ارز رمزنگاری شده برای بیش از سه سال استفاده می کند. ما وجود تاثیر تغییرات را شناسایی می کنیم، که برای نمونه های کوتاه مدت بسیار قابل توجه است اما در درازمدت از بین می رود. سپس، ما نشان می دهیم که همبستگی متقابل بازده هفتگی بین نمونه تغییر ارز های رمزنگاری شده و دارایی های سنتی برخلاف همبستگی بازده بین دارایی های سنتی است. در آخر، ما می دانیم که نمونه تغییر ارزهای رمزنگاری شده نه تنها مزایای ایجاد تنوع را ارائه می دهد بلکه می تواند یک مانع و یک پناهگاه امن برای دارایی های سنتی باشد.

1. مقدمه

بازار ارز رمزنگاری شده به یک مسئله سرمایه گذاری مکرر تبدیل شده و به همین دلیل، رشد چشمگیری در تحقیقات صورت گرفته است که درصدد درک ماهیت این بازار هستند. تاکنون مقالات تجربی دانش ما را در مورد رفتار و ویژگی های ارزهای رمزنگاری شده به طور قابل توجهی بهبود بخشیده اند. به طور خاص، ارزهای رمزنگاری شده تمایل دارند روندهای حافظه طولانی را دنبال کنند (Phillip و همکاران، ۲۰۱۸)، اما در میزان کارآیی اطلاعاتی (در داخل) متفاوت هستند (Urquhart، ۲۰۱۶؛ Bariviera، ۲۰۱۷؛ Nadarajah and Chu، ۲۰۱۷). ارزهای رمزنگاری شده هیچ ارزش ذاتی ای ندارند و بنابراین نسبت به سایر ارزها برای حباب های سوداگرانه مستعدتر هستند (Cheah and Fry، ۲۰۱۵). ارزهای رمزنگاری شده بسیار ریسک پذیر (Pelster و همکاران، ۲۰۱۹) و فرار هستند (Dwyer، ۲۰۱۵؛ Katsiampa، ۲۰۱۷؛ Chaim and Laurini، ۲۰۱۸) و می توانند برای معامله گران سوداگر جذاب باشند (de la Horra و همکاران، ۲۰۱۹). نکته قابل توجه، آنها می توانند به معامله گرانی سود دهند که انتظار دارند برندگان گذشته برندگان آینده شوند و بازندگان گذشته به باختن در آینده ادامه دهند. (Kristoufek، ۲۰۱۳؛ Grobys و Sapkota، ۲۰۱۹). این نشان دهنده معاملات لحظه ای است، که دارایی های کوتاه مدت بدترین عملکرد را دارند و دارایی های بلندمدت در جایگاه بهتری هستند (Jegadeesh و Titman، ۱۹۹۳).

به موازات تحقیقات متقابل تجارت در سهام، ارزهای خارجی و بازارهای کالایی (به عنوان مثال Miffre و Rallis، ۲۰۰۷ ؛ Menkhoff و همکاران، ۲۰۱۲)، ارز رمزنگاری شده یک زمینه پرسود برای استراتژی های تغییر فراهم می کند. ابتدا، ارزهای رمزنگاری شده در بسیاری از سیستم عامل های تجاری (به عنوان مثال، Etoro.com) محدودیت های فروش کوتاه مدت ندارند. دوم، استراتژی های تغییر به دلیل هزینه های ناچیز مورد نیاز برای ذخیره دارایی های دیجیتال جذاب هستند. سوم، مطابق Bitinfocharts.com هزینه معاملات پایین بوده و بسته به بستر مبادله بازار متفاوت است. از این رو، بعید است بازده حاصل از معاملات لحظه ای تحت تأثیر هزینه های اجرای استراتژی قرار گیرد. به بهترین دانش ما، فقط Grobys و Sapkota (۲۰۱۹) معاملات لحظه ای در بازار ارزهای رمزنگاری شده را بررسی می کنند. در Grobys و Sapkota (۲۰۱۹)، استراتژی های معاملات دوره تشکیل ۱۲، ۶ و ۱ ماهه و یک دوره برگزاری ۱ ماهه را شامل می شود. جالب اینجاست که آنها هیچ مدرکی مبنی بر بازده قابل ملاحظه ای پیدا نمی کنند. یک توضیح قابل قبول این است که بازده ارز رمزنگاره شده بسیار بی ثبات است (Baek و Elbeck، ۲۰۱۵)، که ممکن است اثرات معکوس داخلی ماهانه را ایجاد کند. با توجه به این توضیحات، استراتژی های تغییر ما از آنها برای بهره برداری از دوره های کوتاه مدت استفاده می کنیم.

بخش دیگری از مقاله، که اخیراً به عنوان نقطه عطفی در تحقیقات ارز های رمزنگاری شده تبدیل شده است، بررسی می کند که، چگونه ارزهای رمزنگاری شده با دارایی های مالی سنتی در ارتباط هستند. در همین راستا، Platanakis و Urquhart (۲۰۱۹b) دریافتند که ارزهای رمزنگاری شده می توانند کاندیداهای عالی برای یک سبد دارایی متنوع و مناسب باشند و ممکن است مزایای ایجاد تنوع را برای سرمایه گذاری های کوتاه مدت ارائه دهند (Corbet  و همکاران، ۲۰۱۸). علاوه بر این، در حالی که بیت کوین از دارایی های سنتی جدا شده است (Baur و همکاران، ۲۰۱۸)، همبستگی عقب مانده با آنها را نشان می دهد (Corbet  و همکاران، ۲۰۱۹).

در برابر این پیش زمینه، آزمایش می کنیم که آیا استراتژی های تغییر کوتاه مدت بازده مثبتی دارند و تنوع، موانع و یا مزایای پناهگاه امن آنها را برای سرمایه گذاران کشف می کنیم.

ما چهار سهم داریم. اول، با طراحی و استفاده از استراتژی های تغییر کوتاه مدت (حداکثر ۱ ماه)، این مطالعه از Grobys و Sapkota (۲۰۱۹) که مرکز استراتژی های تغییر بیشتر از ۱ ماه قرار دارند، جدا می شود. دوم، بر خلاف Grobys وSapkota (۲۰۱۹)، در جایی که نمونه های تغییر نمی توانند براساس ریسک تنظیم شوند، ما میزان ریسک را بر اساس نرخ بهره بدون ریسک در نظر می گیریم و نمونه های تغییری خود را با ضریب تعدیل ریسک مقیاس می کنیم. سوم، استراتژی های تغییر در این عامل مطالعه در هزینه معقول معامله، و بنابراین بیشتر با شرایط دنیای واقعی پیرامون تصمیمات سرمایه گذاران ارز های رمزنگاری شده می شوند. چهارم، تحقیقات ما به مقالاتب که مزایای ایجاد تنوع را ارزیابی می کنند (مثلاً، Platanakis  و Urquhart، ۲۰۱۹a) و خصوصیات مانع و پناهگاه امن ارزهای رمزنگاری شده (مثلاً بوری و همکاران، ۲۰۱۷a,b) کمک می کند. با این حال، در حالی که بوری و همکارانش (۲۰۱۷a,b) به طور خاص روی بیت کوین تمرکز می کنند، می پرسیم که آیا ویژگی های ذکر شده در بالا به سبد خرید ارزهای رمزنگاری شده اعمال می شود یا خیر.

2. داده و روش

نمونه ما شامل قیمت های بسته شدن روزانه در بازه زمانی ۱/۱۲/۲۰۱۵ تا ۲۹/۱/۲۰۱۹ برای ۱۲ ارز رمز نگاری شده از Coinmarketcap.com است. این انتخاب براساس (i) ارزهای رمزنگاری شده با بیشترین سرمایه در بازار است (به جدول ، Mcap >۱۰۰ میلیون دلار مراجعه کنید) و (ii) داشتن بیش از سه سال داده. بنابراین، نمونه های تغییر تعداد کافی از مشاهدات را برای استنباط معنی دار ما فراهم می کند. جدول ۱ و شکل ۱ بازده روزانه این ارزهای رمزنگاری شده را نشان می دهد.

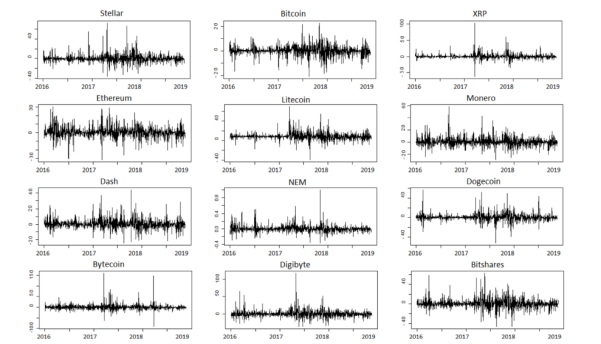
شکل ۱. بازده ارز های رمزنگاری شده. توجه: بازده روزانه در ۱۲ ارز رمزنگاری شده نمایش داده می شود. بازده به عنوان برگشتی( بازده = ۱۰۰ ∗ ln ( ۱Pricet / Pricet −) )محاسبه می شود. محور افقی نشانگر زمان از ۱/۱۲/۲۰۱۵ تا ۲۹/۱/۲۰۱۹ و محور عمودی درصد بازده است.

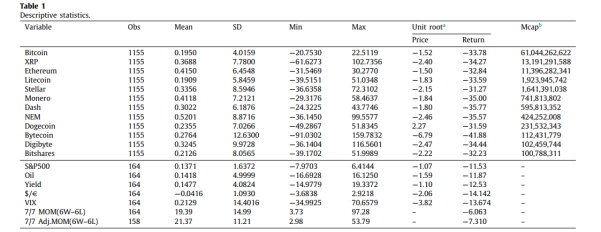
ما از استراتژی موسوم به (J / K) Jegadeesh and Titman، ۱۹۹۳ برای ساخت نمونه های تغییر استفاده می کنیم، جایی که J دوره شکل گیری است (در تعداد روز) و K مدت زمان برگزاری است. این استراتژی براساس بازده تجمعی طی روزهای گذشته J، ارزهای رمزنگاری شده را انتخاب می کند. در آغاز روز t، ارزهای رمزنگاری شده بر اساس بازده آنها در روزهای گذشته J به ترتیب نزولی قرار می گیرند. براساس این رتبه بندی ها، ۱۲ ارز رمزنگاری شده به دو سبد تقسیم می شوند. نمونه “برندگان” (برندگان) یک نمونه کار مشابه وزن از ۶ ارز رمزنگاری شده برتر است، در حالی که نمونه “بازنده ها” (بازندگان) یک نمونه به همان اندازه وزن ۶ ارز رمزنگاری شده پایین است. برای استحکام، ما همچنین ۳ ارز رمز نگاری شده برتر و۳ ارز رمزنگاری شده از آخر را در نظر می گیریم. استراتژی تغییر، نمونه برنده  و بازنده را خریداری می کنند، MOM = برندگان − بازنده ها را می فروشد و MOM بازده درصد هفتگی از سبد تغییر است. این موقعیت را در روز t + K  می بندد. سپس بازده تجمعی در ارزهای انفرادی طی روزهای J گذشته محاسبه می شود.

 علاوه بر این، به طور مشابه با Barroso و Santa-Clara (۲۰۱۵)، ما یک نمونه تغییر تنظیم ریسک ایجاد می کنیم. برای این منظور، یک نمونه تغییر برای هر دو نرخ بدون ریسک (RF) و هزینه معاملات (TC) تنظیم می شود. در مرحله دوم، Brauneis و Mestel (۲۰۱۸)، Kraken.com و Bitinfocharts.com برای هر تجارت ۲۶ امتیاز پایه دارند.

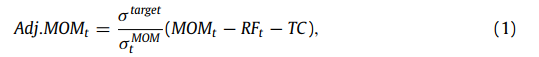
 که در آن MOM همانطور که قبلاً تعریف شده بازده نمونه تغییر(اندازه گیری نشده) است. این استراتژی مدیریت ریسک از نوسانات متوسط فراریت (σtMOM) نسبت به شش دوره قبلی به منظور هدف قرار دادن نوسانات ثابت (σtarget) استفاده می کند. نسبت (σtarget/ σtMOM) نشان می دهد که در دوره های کم (زیاد) نوسانات در بازار، معامله گران حرکت مقادیر بزرگتر (کوچکتر) را در نمونه تغییر (غیرقابل استفاده) سرمایه گذاری می کنند. در نتیجه، بازده در نمونه تغییر تنظیم تعدیل ریسک ناپایدار می شود. شایان ذکر است که یک تغییر لحظه ای با ساختن یک استراتژی کوتاه مدت ۱۰۰٪ توسط خود تأمین می شود، که بدون فرض هزینه های اهرم قابل مقیاس است.

اکنون همبستگی های پویا بین یک نمونه تغییر ارز رمزنگاری شده و سایر دارایی های سنتی در فرکانس هفتگی (J / K = ۷/۷) را بررسی می کنیم. برای این منظور، ما از یک مدل VAR ()  -DCC-MGARCH  (، ۱) استفاده می کنیم، که شامل همبستگی های شرطی پویا است، که توسط Engle  سال ۲۰۰۲ توسعه داده شده است. اگرچه مطالعات تجربی با استفاده از مدلهای بهینه سازی نمونه ها، تجزیه واریانس تعمیم یافته و معیارهای عملکردی مختلف، ویژگی های ریسک و بازده ارزهای رمزنگاری شده را به عنوان دارایی های مالی مورد بررسی قرار داده است (Corbet و همکاران، ۲۰۱۸؛ Platanakis و همکاران، ۲۰۱۸؛ Phillip وهمکاران، ۲۰۱۸) VAR ()-DCC-MGARCH (، ۱) می تواند برای سه دلیل بعدی یک تصویر مفصل تر ترسیم کند. اول، آن را برای تشخیص تغییرات در طول زمان در همبستگی ها مجهز کرده است. دوم، آن پراکندگی ناپایداری پویا بین بازده دارایی غیرقابل پیش بینی را بررسی می کند. سوم، ناهمگونی و نوسانات زیاد را کنترل می کند.

فرض می کنیم که مدل میانگین شرطی تجزیه VAR (۱) به شرح زیر است:

Yt یک بردار mبعدی است که شامل درصد بازده هفتگی دارایی های سنتی است. به طور خاص، مطابق با Bouri و همکاران (۲۰۱۷b) و Corbet و همکاران (۲۰۱۸)، ما شاخص کامپوزیت S&P۵۰۰ (S & P۵۰۰)، نفت خام (Oil)، عملکرد ۱۰ ساله به سررسید اوراق خزانه داری (بازده)، نرخ ارزEUR / USD ($ / e) و شاخص نوسانات سهام S & P۵۰۰ را درگزینه های فهرست (VIX) نظر می گیریم . داده های مربوط به این متغیرها از Datastream بازیابی می شوند. ما همچنین می خواهیم بازده نمونه تغییر (MOM) را اضافه کنیم.Yt−  شامل بازده های تاخیر است، €t یک بردار از اصطلاحات آشفتگی تصادفی است، vt یک بردار از نوآوری های عادی است که بطور یکسان و مستقل توزیع شده است، و Ht واریانس شرطی و ماتریس کواریانس است:

در اینجا Dt یک ماتریس مورب از واریانس های شرطی از GARCH (،۱) یک متغیره است، و Rt ماتریس همبستگی متغیر تغییر زمان است (برای مطالعه بیشتر به Engle مراجعه کنید، ۲۰۰۲).

برای اینکه بطور رسمی ارزیابی کنیم که آیا می توان یک نمونه تغییر ارز رمزنگاری شده را به عنوان یک تقسیم کننده، مانع یا پناهگاه امن در نظر گرفت ، معادله رگرسیون OLS زیر را در نظر می گیریم (Ratner and Chiu، ۲۰۱۳؛ Bouri و همکاران، ۲۰۱۷a,b):

در اینجا DCCt همبستگی شرطی پویا دو طرفه (یک عنصر خارج از مورب Rt ماتریس) بین تغییر۷/۷ (۶W-۶L) و هر دارایی سنتی دیگر است. DUM یک متغیر ساختگی است ، که در صدک های پایین (۱ ، q = ۱۰٪ ، ٪ و ٪) از توزیع بازده دارایی سنتی ، ارزش ۱ را به خود اختصاص می دهد. براساس اصول کلی ، دارایی به عنوان یک تعدیل کننده (مانع ضعیف ، مانع قوی) در نظر گرفته می شود ، اگر به طور متوسط ، به ترتیب به طور مثبت (بدون همبستگی ، همبستگی منفی) با دارایی یا سبد دیگر مرتبط باشد. در حالی که اگر یک دوره منفی یا بدون همبستگی با دارایی دیگر در یک دوره آشفتگی نشان دهد ، به عنوان یک پناهگاه امن تلقی می شود (Ratner و Chiu، ۲۰۱۳). از این رو ، اگر اصطلاح ثابت (a) مثبت و معنادار باشد (ناچیز ، منفی و قابل توجه) ، می توان نمونه تغییر ارز رمزنگاری شده را به عنوان یک تغییر دهنده (مانع ضعیف ، مانع قوی) درک کرد (Bouri و همکاران ، ۲۰۱۷a,b). اگر ضرایب a ، a و a ناچیز یا منفی باشند ، نمونه تغییرات یا به ترتیب ضعیف یا یک پناهگاه امن قوی در برابر تغییرات در دارایی یا سبد دیگر به ترتیب است (Bouri و همکاران ، ۲۰۱۷a,b).

3. نتایج تجربی

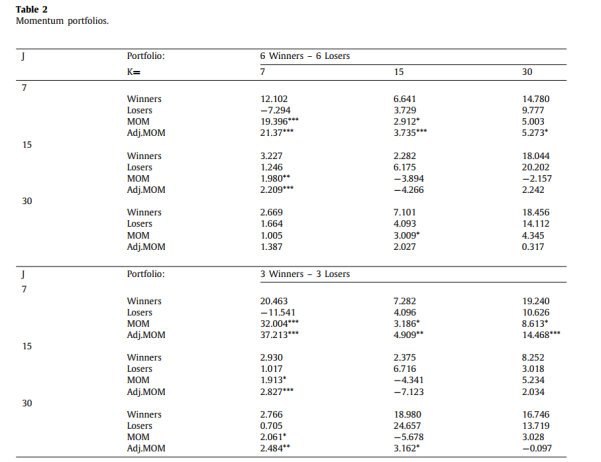
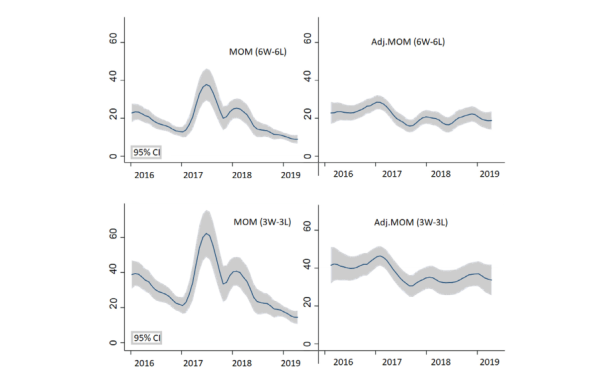
این بخش را با گزارش استراتژی های تغییر شروع می کنیم. جدول ، ۹ استراتژی تغییر را با مقادیر J و K در ، ۱۵ و ۳۰ روز نشان می دهد. اگرچه نمونه برندگان به طور کلی بر بازنده ها تسلط دارد ، نتایج فقط برای تغییر کوتاه مدت (۷/۷ ، ۷/۱۵ ، ۷/۳۰ و ۱۵/۷) قابل توجه است ، که بخشی از یافته های گزارش شده در Grobys و Sapkota (۲۰۱۹) را اثبات می کند. . استراتژی ۷/۷ سودآورترین است؛ این نرخ بازده هفتگی ۱۹٪ را دارد، که ۱۲٪ از آنها به موقعیت طولانی برندگان و ٪ به موقعیتی کوتاه از بازندگان اختصاص می یابد. ما همچنین سودآوری معاملات حرکت را در ۳ ارز رمزنگاری شده ابتدای جدول و ۳ ارز رمزنگاری شده در آخر جدول را بررسی می کنیم. به همین ترتیب، استراتژی ۷/۷ بازده مثبت و معنادار ۳۲٪ را به همراه دارد. با کنترل ناپایداری و هزینه های معامله ، بازده تغییر کوتاه مدت مثبت و قابل توجه باقی می ماند ( به Adj.MOM در جدول ۲ مراجعه کنید). همانطور که انتظار می رفت (Barroso و Santa-Clara، ۲۰۱۵)، Adj.MOM از نظر MOM بالاتر است ، گواهی می دهد که استراتژی پیشنهادی مدیریت ریسک از سوداگران شتاب در بازار ارز رمزنگاری شده سود می برد. در این راستا ، شکل ۲ نشان می دهد که چگونه بازده در استراتژی ۷/۷ در طی یک دوره ۱۶۴ هفته (۰۹/۱۲ / ۲۰۱۵-۲۹ / ۱/۲۰۱۹) باز می گردد.

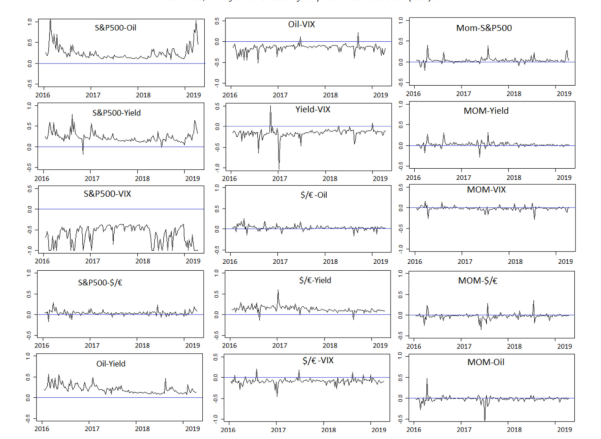
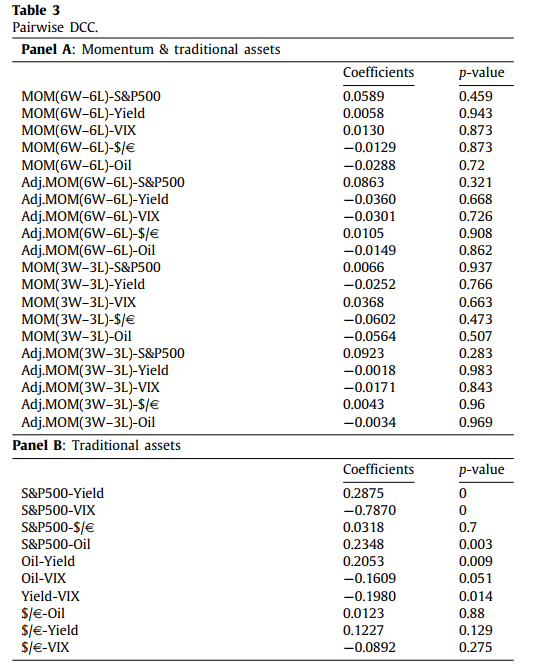
اکنون بررسی می کنیم که آیا بازده تغییر با دارایی های سنتی در ارتباط است (جدول ۳ و شکل ۳ را ببینید). ما می دانیم که ارتباط بین دارایی های سنتی با صفر تفاوت دارد (جدول ۳ ، پانل B). به عنوان مثال ، DCC بین S & P۵۰۰– Yield ، S & P۵۰۰-VIX ، S & P۵۰۰-Oil ، Oil-Yield ، Oil-VIX و Yield-VIX با ضرایب ۲۹٪ ، ۷۹ − ، ۲۳٪ ، ۲۱٪ ، ۱۶٪ و به ترتیب ۲۰٪ در مقابل ، به نظر می رسد تغیییر از دارایی های سنتی (پانل A) جدا می شود ، جایی که همبستگی ها ناچیز هستند و بین ٪ تا ۹.۲ متغیر هستند. در نتیجه ، یک نمونه تغییر از ارزهای رمزنگاری شده را می توان وسیله ای برای تنوع ریسک در نظر گرفت.

علاوه بر این ، جدول ۴ نشان می دهد که یک نمونه تغییر از ارزهای رمزنگاری شده می تواند هم مانع قوی (منفی A۰) باشد و هم یک پناهگاه ضعیف (با نامرئی A۱ ، A۲ و a۳) در برابر حرکات جانبی در نفت، بازده ، $ / e و VIX. یک نمونه از تغییر ارزهای رمزنگاری شده نیز می تواند یک تغییر دهنده (مثبت a۰) و یک پناهگاه امن قوی (منفی a۲) در برابر تغییرات در S&P۵۰۰ باشد.

4. نتیجه گیری

این مقاله به بررسی عملکرد استراتژی های تغییر در بازار رمزنگاری شده و به بررسی تنوع و مزایای حمایت از تجارت تغییر می پردازد. ما نشان می دهیم که بازده مثبت می تواند از استراتژی های تغییر در کوتاه مدت حاصل شود. این یافته همراه با تحقیقات قبلی (Grobys و Sapkota، ۲۰۱۹) دلالت بر این دارد که بازار رمزنگاری شده در کوتاه مدت و در درازمدت ناکارآمد است. همبستگی بازده بین نمونه تغییر ارزهای رمزنگاری شده و دارایی های سنتی پایین تر از همبستگی بین دارایی های سنتی است. بنابراین ، سرمایه گذاران باید یکنمونه تغییر از ارزهای رمزنگاری شده را به عنوان وسیله ای برای تنوع ریسک و یا محافظت در نظر بگیرند. تحقیقات آینده باید بهینه سازی نمونه ها را با استراتژی های تغییر انجام دهد ، جایی که همبستگی های متغیر زمان می تواند منجر به ایجاد مجدد یک نمونه متنوع دارایی شود.